“方べきの定理2”の公式とその証明です!
方べきの定理2
公式
方べきの定理2二直線の1直線と円の交点をA、Bとし、もう1直線と円がTで接するとき
\(PA・PB=PT^2\)

証明
三角形の相似による証明
証明
接弦定理より
∠PTA=∠PBT
また∠Pが共通であるため
△PTA∽△PBT
よって
PT:PA=PB:PT
よって
\(PA・PB=PT^2\)
問題
Q
図のPAを求めよ。
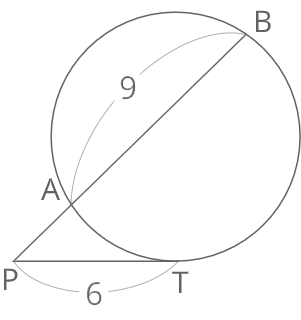
A
方べきの定理2より
\(PA・PB=PT^2\)
⇒\(PA・(PA+AB)=PA・(PA+7)=PT^2=6^2=36\)
⇒\(PA^2+9PA-36=0\)
⇒\((PA+12)(PA-3)=0\)
よって
\(PA=3\)
まとめ
円と直線の組み合わせが出てきたときには方べきの定理が使えるかもしれないので,使えるようにしておきましょう。




