“メネラウスの定理”の公式とその証明です!
メネラウスの定理
公式
メネラウスの定理直線lとBC、CA、ABの交点をそれぞれP、Q、Rとすると
\(\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=1\)
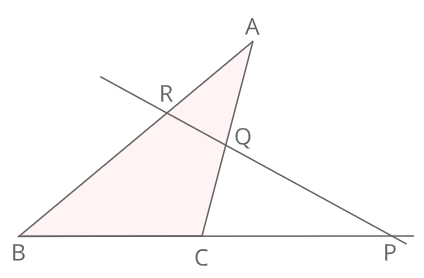
証明
面積比による証明
証明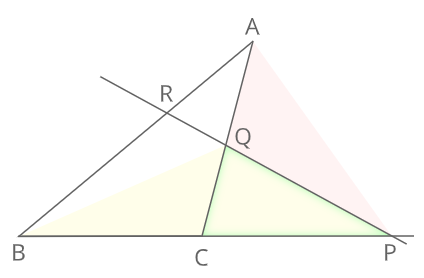
△BPQと△PCQは高さが同じであるため面積比は
△BPQ:△PCQ=BP:PC
⇒\(\frac{BP}{PC}=\frac{△BPQ}{△PCQ}\) ①
△PCQと△PAQは底辺QPを底辺とするとそれぞれの高さはCQ:QAの関係にあるため
△PCQ:△PAQ=CQ:QA
⇒\(\frac{CQ}{QA}=\frac{△PCQ}{△PAQ}\) ②
また△PAQと△BPQは底辺QPを底辺とするとそれぞれの高さはAR:RBの関係にあるため
△PAQ:△BPQ=AR:RB
⇒\(\frac{AR}{RB}=\frac{△PAQ}{△BPQ}\) ③
①、②、③の積より
\(\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=\frac{△BPQ}{△PCQ}・\frac{△PCQ}{△PAQ}・\frac{△PAQ}{△BPQ}=1\)
よって
\(\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=1\)
問題
Q
図のPCを求めよ
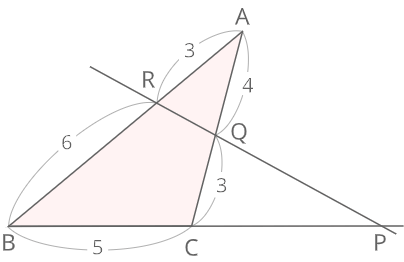
A
メネラウスの定理より
\(\frac{BP}{PC}・\frac{3}{4}・\frac{3}{6}=1\)
\(\frac{5+PC}{PC}・\frac{3}{4}・\frac{3}{6}=1\)
\(9(5+PC)=24PC\)
\(45=15PC\)
⇒\(PC=3\)となります.
まとめ
三角形に直線が交わっている場合はメネラウスの定理が使えることもあるので,しっかりと使えるようにしておきましょう.



