“加法定理”の公式とその証明です!
加法定理
公式
加法定理\(・sin(α+β)=sinαcosβ+cosαsinβ\)
\(・sin(α-β)=sinαcosβ-cosαsinβ\)
\(・cos(α+β)=cosαcosβ-sinαsinβ\)
\(・cos(α-β)=cosαcosβ+sinαsinβ\)
\(・tan(α+β)=\frac{tanα+tanβ}{1-tanαtanβ}\)
\(・tan(α-β)=\frac{tanα-tanβ}{1+tanαtanβ}\)
証明
\(cos(α+β)\)の証明
証明 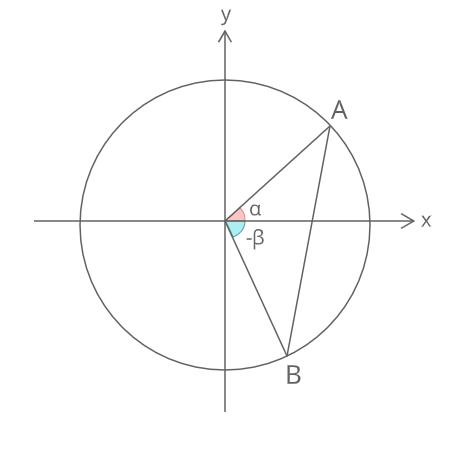
2点A(cosα, sinα)、B(cos(-β), sin(-β))の距離ABは
\(AB^2\)
\(=(cosα-cos(-β))^2+(sinα-sin(-β))^2\)
\(=(cos^2α+sin^2α)+(cos^2(-β)+sin^2(-β))\)
\(-2cosαcosβ+2sinαsinβ \)
\(=2-2cosαcosβ+2sinαsinβ ① \)
また余弦定理より
\(AB^2\)
\(=1^2+1^2-2×1×1×cos(α+β)\)
\(=2-2cos(α+β) ②\)
①、②より
\(2-2cosαcosβ+2sinαsinβ=2-2cos(α+β)\)
よって
\(cos(α+β)=cosαcosβ-sinαsinβ\)
\(cos(α-β)\)の証明
証明
\(cos(α-β)\)
\(=cos(α+(-β))\)
\(・cos(α+β)=cosαcosβ-sinαsinβ\)より
\(=cosαcos(-β)-sinαsin(-β)\)
また\(cos(-β)=cosβ、sin(-β)=-sinβ\)なので
\(=cosαcosβ+sinαsinβ\)
\(sin(α+β)\)の証明
証明
\(sin(α+β)\)
\(・sinθ=cos(θ-\frac{π}{2})\)より
\(=cos((α+β)-\frac{π}{2})\)
\(=cos(α+(β-\frac{π}{2}))\)
\(=cosαcos(β-\frac{π}{2})-sinαsin(β-\frac{π}{2})\)
また\(cos(θ-\frac{π}{2})=sinθ\)\(、sin(θ-\frac{π}{2})=-cosθ \)なので
\(=cosαsinβ+sinαcosβ\)
\(=sinαcosβ+cosαsinβ\)
\(sin(α-β)\)の証明
証明
\(sin(α-β)\)
\(=sin(α+(-β))\)
\(・sin(α+β)=sinαcosβ+cosαsinβ\)より
\(=sinαcos(-β)+cosαsin(-β)\)
\(=sinαcosβ-cosαsinβ\)
\(tan(α+β)\)の証明
証明
\(tan(α+β)\)
\(=\frac{sin(α+β)}{cos(α+β)}\)
\(・sin(α+β)=sinαcosβ+cosαsinβ\)と
\(・cos(α+β)=cosαcosβ-sinαsinβ\)より
\(=\frac{(sinαcosβ+cosαsinβ)÷(cosαcosβ)}{(cosαcosβ-sinαsinβ)÷(cosαcosβ)}\)
\(=\frac{tanα+tanβ}{1-tanαtanβ}\)
\(tan(α-β)\)の証明
証明
\(tan(α-β)\)
\(=\frac{sin(α-β)}{cos(α-β)}\)
\(・sin(α-β)=sinαcosβ-cosαsinβ\)と
\(・cos(α-β)=cosαcosβ+sinαsinβ\)より
\(=\frac{(sinαcosβ-cosαsinβ)÷(cosαcosβ)}{(cosαcosβ+sinαsinβ)÷(cosαcosβ)}\)
\(=\frac{tanα-tanβ}{1+tanαtanβ}\)




